不等式数独

什么是不等式数独？

不等式数独（Futoshiki）是一款富有挑战性的逻辑推理游戏，起源于日本，也被称为“比较数独”。它的规则类似于数独，但增加了“大于（>）” 和 “小于（<）”的比较关系，让解题过程更加烧脑！

游戏规则：

• 每行、每列的数字不能重复出现。
• 不等式符号（> 或 <） 约束了相邻单元格的大小关系。
• 目标是按照规则填满整个网格，确保所有不等式都成立。

如何玩不等式数独？

1. 选择网格大小（3×3, 4×4, … 9×9），网格越大，难度越高。
2. 选择难度级别（简单 / 中等 / 困难），决定初始给定的数字和不等式数量。
3. 根据已填入的数字和不等式关系，推理出空白格的正确数字。
4. 系统会自动检测错误，错误的填法会被标记提醒。
5. 成功填满所有数字，且满足所有规则，即可通关！

辅助功能：

• “答案” 按钮：查看当前谜题的完整解法。
• “重置” 按钮：回到初始状态，重新挑战。

高效解题技巧：如何快速通关？

1. 先从不等式入手，找出最大值或最小值

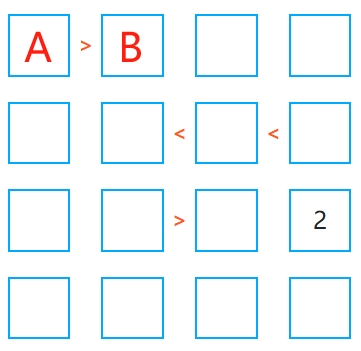
看到 A > B 时，A 不能是最小值，B 不能是最大值。例如，在 4×4 网格中，数字范围是 1-4，如果 A > B，那么 B 不可能是 4，A 也不会是 1。

2. 先填“唯一可能”的数字

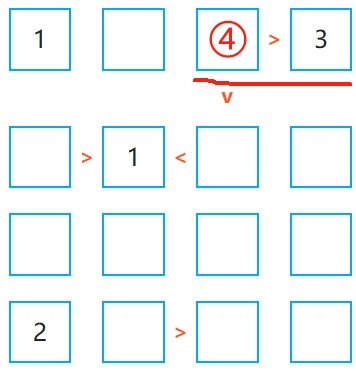
某一行或某一列只剩下一个空格时，它的数值是唯一确定的，可直接填入。如果某个空格只有一个数符合不等式关系，那它也是唯一解。

3. 利用行列排除法，逐步缩小候选值

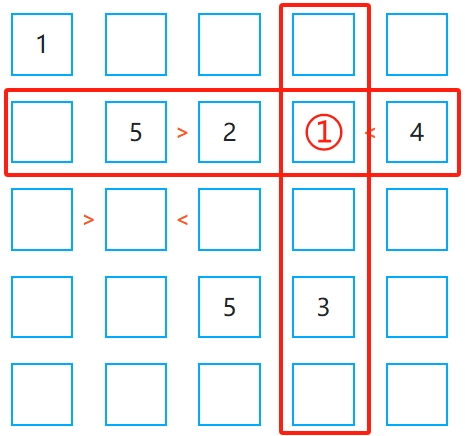
由于每行、每列的数字不能重复，可以通过排除法找到可能的填充值。例如，在 5×5 网格 中，某行已有 1, 2, 4, 5，那么剩下的空格只能填 3。

4. 观察不等式链，推导数字范围

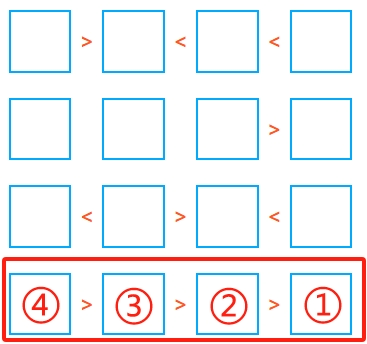
如果出现 A > B > C > D 这种连续不等式，可以直接推断它们的取值范围！例如，在 4×4 网格中，A 只能是 4，B 只能是 3，C 只能是 2，D 只能是 1。

5. 遇到复杂情况，使用“回溯法”

尝试填入一个可能的数字，然后继续推理，看看是否出现矛盾。如果出现矛盾，就回退到上一步，尝试其他可能的解。

常见问题

• Futoshiki 和数独有什么不同？

  传统数独仅要求“每行每列不重复”，而 Futoshiki 额外增加了不等式关系，增加了推理难度。

• 为什么填入数字会出现红色背景？

  这是系统提示填入的数字有误，可能的错误包括：

  • 此行或此列出现了重复数字。
  • 填入的数字不满足 “>” 或 “<” 关系。

• 怎样才能更快地解题？

  从不等式线索入手，结合唯一性、排除法和逻辑推理，逐步缩小候选数字范围。

• “简单”、“中等”、“困难” 的区别是什么？

  难度级别影响初始提示数量，简单模式会有更多已填入的数字和更少的不等式关系；而困难模式给出的线索更少，同时会有更多的不等式约数关系。